Contents

Introduction

Naïvely, many-body quantum wave functions contain an exponential amount of information: for example, the quantum state of N spin-1/2 particles can be fully described using $2^N$ complex numbers. Given the memory constraints of real computers, such a complete description is only possible for small systems. However, quantum states of physical interest, such as the ground states of condensed-matter systems, are highly structured and can be compressed using an appropriate representation. The parameters of these variational ansätze can be optimised to represent ground states using variational Monte Carlo, or to track the time evolution of a state using the time-dependent variational principle.

Building on the success of deep neural networks at representing images, language, and other types of information motivates using them as a variational ansatz. In such a neural quantum state, the network takes a computational basis state as its input and outputs its amplitude in the wave function $|\psi\rangle$. For example, a many-body spin-1/2 quantum state can be written in the $\sigma^z$ basis as

$$ |\psi\rangle = \sum_{\sigma_1,\dots = \pm1} \psi(\sigma_1,\dots) |\sigma_1,\dots\rangle; $$

the neural network is used to encode the function $\psi(\sigma_1,\dots)$.

Neural quantum states have been used successfully for a variety of challenging problems in many-body quantum physics. Nevertheless, it is a new method, with many open and challenging tasks to solve in order to bring out its full potential. I am interested in solving these problems, as well as exploiting the improvements to solve open problems in condensed-matter physics.

NQS and the sign problem

Quantum Monte Carlo methods allow us to solve quantum many-body problems numerically exactly. However, they are limited by the Monte Carlo sign problem: the probability distribution used in the Monte Carlo sampling is only fully positive (i.e., a valid probability distribution) for stoquastic Hamiltonians. These include interacting bosons and non-frustrated magnets; by contrast, fermion systems and frustrated magnets are not amenable to quantum Monte Carlo.

I discovered that NQS may show a similar “sign problem”. Ground state wave functions of stoquastic Hamiltonians have all-positive amplitudes: they are equivalent to probability distributions, which are well represented by neural networks. By contrast, learning the ground state of a non-stoquastic Hamiltonian involve destructive interference. NQS architectures that split amplitudes and complex phases of the wave function struggle to follow these interferences, since the phase has to suddenly jump by $\pi$ whenever $\psi=0$. This is a serious issue for such important architectures as recurrent neural networks, which need an explicit representation of the Born probability distribution.

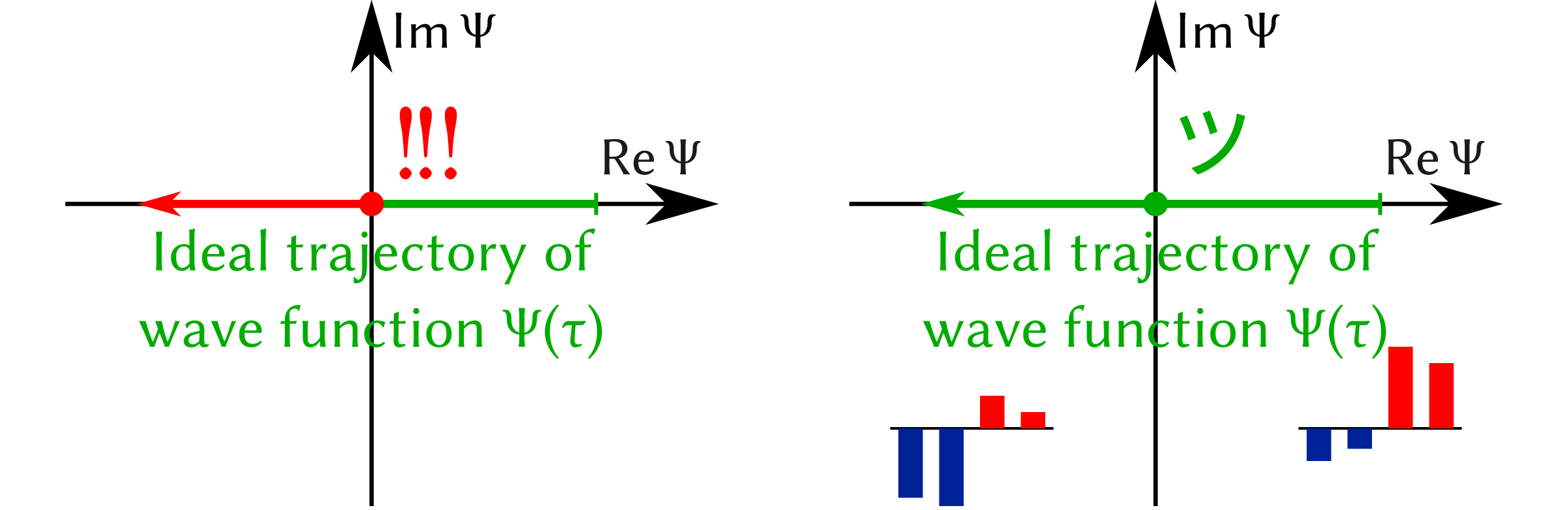
Ansätze with separate wave function amplitudes and phases (left) cannot track destructive interferences. Writing the wave function as a sum of terms (right) improves the issue.

I found later that writing the wave function as a sum of terms allows tracking destructive interference in many cases: $\psi=0$ is no longer special, as it can be crossed by changing the relative magnitude of positive and negative terms. This allowed us to obtain excellent wave functions for such highly frustrated magnets as the $J_1-J_2$ Heisenberg model on the square and triangular lattices. Nevertheless, the sign structures of fermion wave functions is considerably more complex, requiring more sophisticated approaches.

Group convolutional networks

The lattice Hamiltonians studied in condensed-matter physics have many symmetries, which are also respected by their eigenstates. Imposing these symmetries on a variational ansatz simplifies the training procedure by avoiding states with different symmetry quantum numbers, so we can reach lower variational energies and more accurate ground state wave functions. Furthermore, by imposing different symmetry quantum numbers, we can resolve a number of low-energy states, including (Anderson) towers of states, which provide a qualitative signature of ordering already for small systems. By extending this method to system sizes that are too large for exact diagonalisation, we can open a new angle on studying quantum phases and transitions.

Together with Chris Roth, we introduced group-convolutional neural networks (GCNNs) to impose arbitrary spatial symmetries on NQS ansätze. In a standard convolutional neural network, every layer is structured as a replica of the input geometry, and mapping from one layer to the next is identical for all lattice sites. As a result, the whole network is translation equivariant: translating its input translates the entries of all subsequent layers by the same amount. The last layer in particular can be viewed as an NQS ansatz $\psi_0$ evaluated for all translated copies of the input: summing these gives a fully translation-symmetric state, while including phase factors $e^{ik\cdot r}$ allows representing states with any given wave vector $k$.

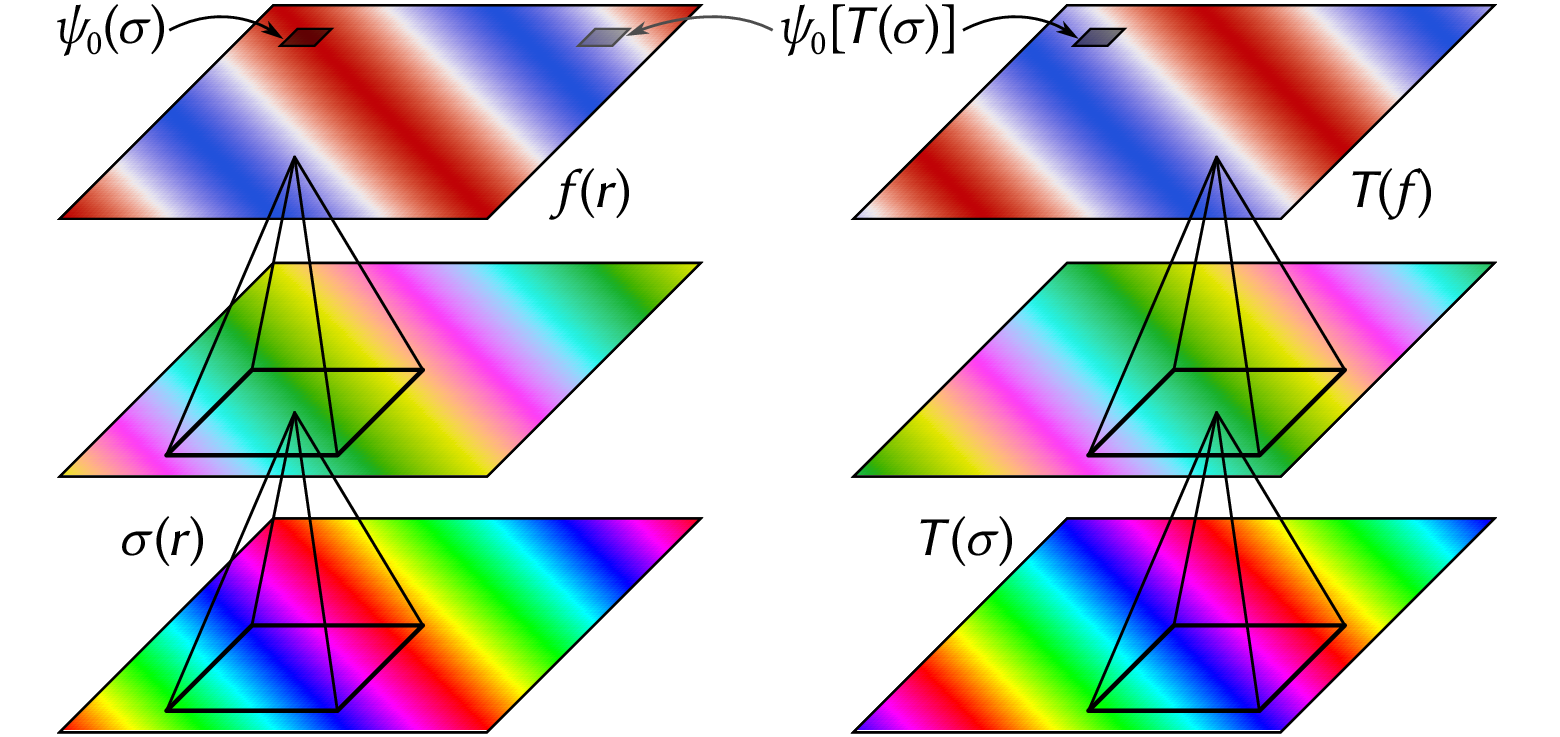
Convolutional neural networks impose translation symmetry.

Group convolutional networks generalise this idea to an arbitrary symmetry group. We now need to evaluate $\psi_0$ for all symmetry-related inputs: since there is one of these for every element of the symmetry group, it makes sense to lay them out according to the geometry of the group. In particular, if we act on the input with a symmetry element, the entries of all subsequent layers are relabelled according to group multiplication. GCNNs use group-equivariant layers to achieve this goal: these first map the input lattice to such group-shaped features, then those to one another.

Group convolutional networks generalise the idea to arbitrary spatial symmetries.

Lattice magnetism

We have first applied the GCNN architecture to the $J_1-J_2$ Heisenberg model on the square and triangular lattices. Both of these models show a variety of ordered phases as well as a possible quantum spin liquid. On the square lattice, our approach has been the first purely neural-network architecture to attain lower variational energies than alternative variational techniques, even on very large systems (up to 16×16 in this work). We were also able to distinguish spin liquid and valence-bond solid phases by measuring dimer correlation functions.

Read more about this project →

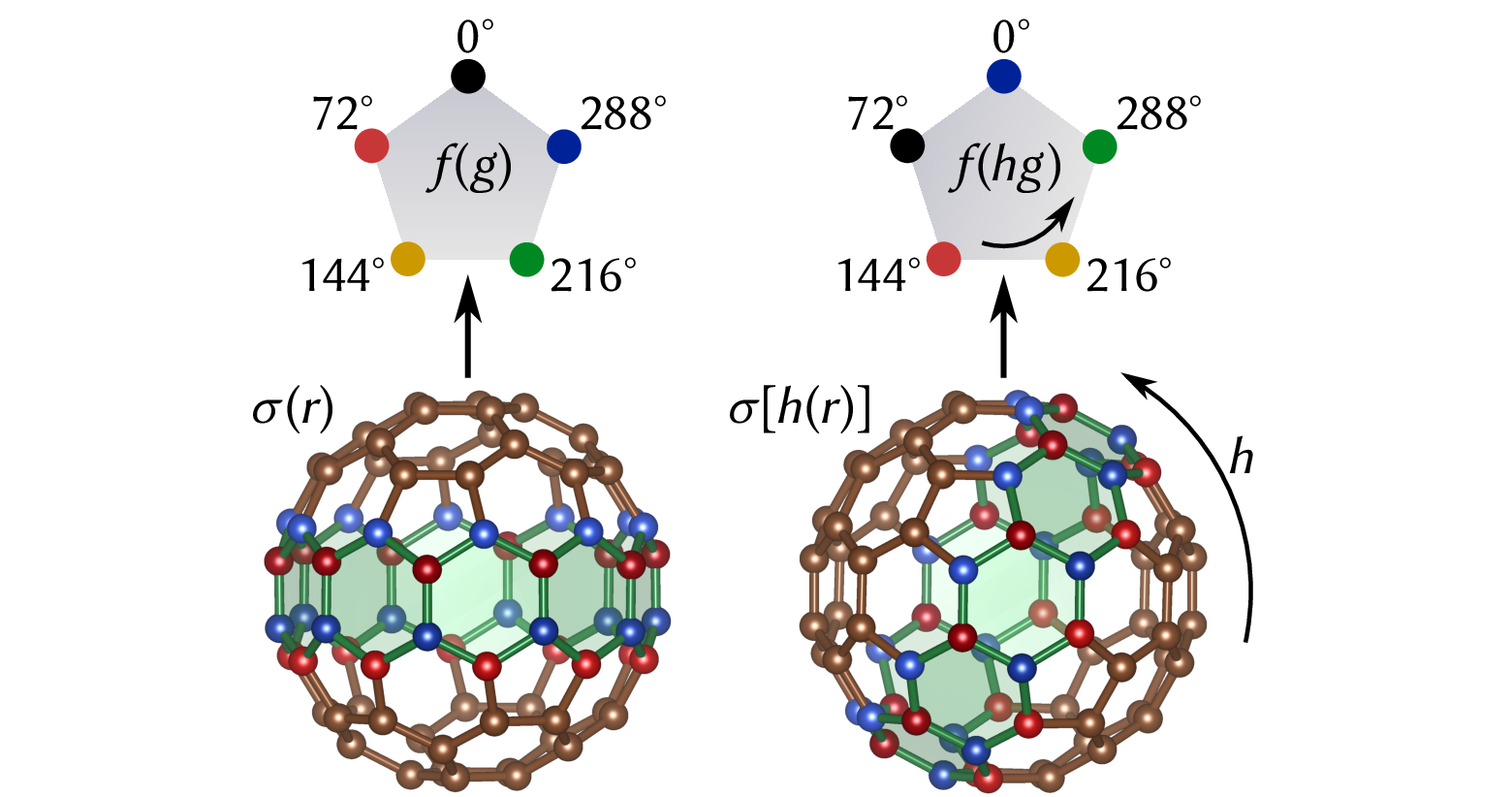
Molecular magnets

Together with Sylvain Capponi and Fabien Alet, we have deployed this method to Heisenberg models on fullerene geometries, which, unlike lattice problems, have no translation symmetry. We were again able to attain excellent variational energies for both the ground state and excited states in different symmetry sectors. Even though the structure is highly frustrated, we found that the ground-state correlation functions show precursors of noncollinear magnetic order, which are also reflected in the low-energy spectrum as a tower of states.

Read more about this project →

NQS for interacting fermions

I am currently interested in extending these ideas to systems of interacting electrons, such as the Hubbard model used to describe high-temperature superconductivity in the cuprates. This poses an extra challenge due to the exchange antisymmetry of fermion wave functions. In practice, imposing this antisymmetry requires the use of Pfaffians or determinants, which generalise mean-field wave functions for superconductors and the normal state, respectively. Neural networks can be used to make the entries of the determinant or the Pfaffian depend on the electron positions, thereby introducing correlations in a flexible way. Such approaches, under the names FermiNet and PauliNet, have shown great results for problems in quantum chemistry.

I work on extending these methods to lattice problems, especially by using group convolutional networks to construct symmetric wave functions at moderate computational cost. However, the fact that fermionic ansätze usually dress a mean-field state make it challenging to represent phases that break these symmetries spontaneously. Surmounting this challenge will allow us to study the low-energy spectrum of Hubbard-type models, which will open a new direction to understand their quantum phases.

Open-source software: NetKet