Research
See below for a non less technical summary of my research interests ↓
My research addresses challenging problems in strongly-correlated-electron systems. In particular, I am interested in the exotic phenomena brought about constrained dynamics in complex energy landscapes, such as fractionalisation and topological order. I pursue these problems using a broad range of analytical techniques, as well as cutting-edge computational tools, and also explore ways to transfer ideas between the two domains. I also collaborate frequently with experiments, especially neutron-scattering studies of magnetism.
My research projects focus on two themes:
- In frustrated magnets, competing interactions bring about unusual magnetic states. I am particularly interested in spin liquids, where frustration disrupts conventional ordering and brings about fractionalised quasiparticles coupled to emergent gauge fields.
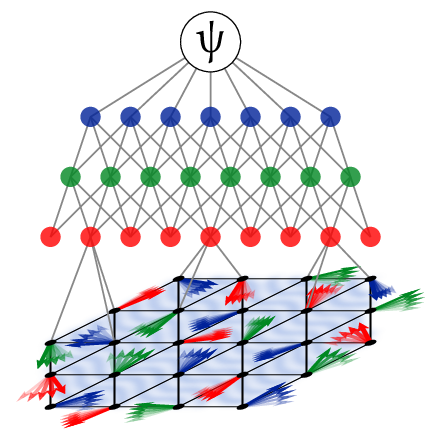
- Representing and working with many-body wave functions is a challenging task on a classical computer. I aim to solve this problem by encoding the wave function in a neural network. In particular, I focus on interference effects and symmetries in these neural quantum states. This has led to very powerful approaches for problems in magnetism; currently, I focus on extending them to systems of interacting electrons.
Find out more about these themes below:
In plain English
More is different. (P. W. Anderson)
All materials are made up of the same ingredients: electrons float around atomic nuclei, bound to them by electromagnetic forces. These ingredients, however, give rise to an incredible variety of material properties: gases, liquids, and solids; insulators and conductors of electricity; magnetism; all of chemistry, and even life! These properties are emergent, that is, they do not belong to a single atom, but only to a large number of them: a single atom is neither solid, nor gas! Furthermore, interactions with their neighbours might completely change the behaviour of single atoms, and bring about new, collective properties. Developing techniques to explain such collective behaviour is one of the main challenges in theoretical physics.
My research focuses on collective behaviour coming from strong interactions between electrons in a solid. This can often be described in terms of “quasiparticles”, in which electrons move together to imitate a free particle. These quasiparticles, however, might be radically different from electrons. My favourite example is fractionalisation, where electrons “split up” into several quasiparticles, which may look completely different from familiar kinds of particle:
- In the fractional quantum Hall effect, the electric charge of an electron splits between 3 (or 5, 7,…) particles, even though charge normally comes in integer multiples of the electron charge.
- In quantum spin liquids, the charge and magnetism of the electron splits into two independent particles. This allows them, for instance, to show all magnetic properties of a metal, while not conducting electricity.
In addition to being interesting on their own right, these exotic quasiparticles helped us explain exciting and important phenomena like high-temperature superconductivity. They can also be used to solve a key challenge in quantum computing. Quantum information is delicate and easily destroyed by noise in the computer. Fractionalised quasiparticles allow us to store and handle quantum information while “hiding” it from noise, thus making quantum computers more robust.
In my work, I study fractionalisation and other exotic phenomena using both traditional theoretical techniques and cutting-edge computational tools. I am particularly interested in using machine learning to simulate the quantum mechanics of strong electron interactions.